Soru 61:
3x + 4y – 24 = 0 doğrusu ve eksenlere 1.bölgede teğet olan çemberin denklemi nedir?
Çözüm:
Soruya uygun bir şekil çizerek soruyu kolayca çözelim;
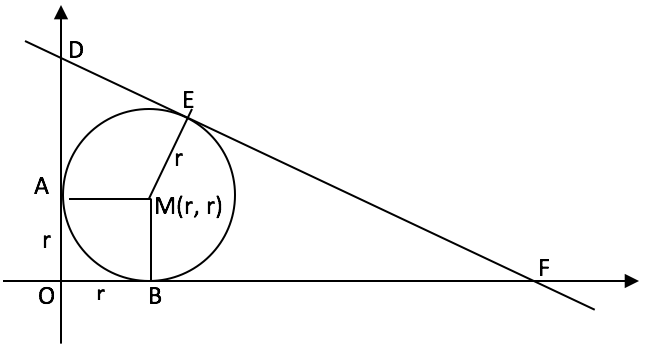
Şekle göre AD = 6-r, DE = 6-r, BF = 8-r, EF = 8-r (Bu değerleri siz de bulun.)
DE+EF = 10 olduğuna (neden?) göre, 6-r + 8-r = 10 
r=2
Merkezin koordinatları (2, 2) ve yarıçap 2olduğuna göre çember denklemi;
(x-2)2 + (y-2)2 = 4 olur.
Dikkat ederseniz soruyu basit çember bilgileri ile çözdük. Analitik çözüm için aşağıdaki soruyu inceleyin.
Soru 62:
Yukardaki soruda çemberimiz 4.bölgede olsaydı, çemberin denklemi ne olurdu?
Çözüm:
Çözüme başlamak için soruya uygun bir şekil çizelim.
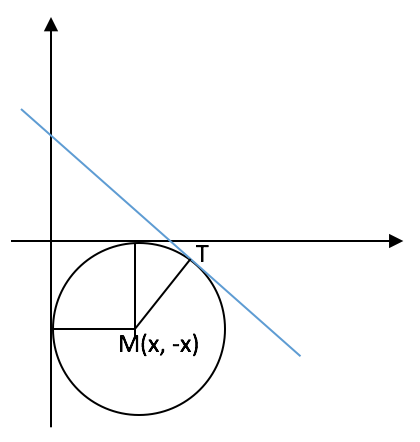
MT uzunluğu da yarıçap olacağına göre, bütün yapılacak iş, bir noktanın bir doğruya uzaklığını veren formülden faydalanarak, x uzunluğunu bulmaktır. (formülü bilmiyorsanız, analitik geometri girişine bakın)
3x + 4y – 24 = 0 denkleminde, a=3, b=4 ve c = -24 ve şekle göre MT = x olacağına göre değerleri formülde yerine koyalım;
eşitliğinden x=6 bulunur.
(Uyarı: Mutlak değer ifadesinin 2 türlü açılacağını biliyorsunuz. Yukardaki eşitlikten x=-4 ve x=6 bulunur ki bize x’in pozitif değeri lazım olduğu için x için 6 değerini aldık.)
Aradığımız çember denklemi; (x-6)2+ (y+6)2 = 36 olur.
(Not: Bir önceki soruyu bu yolla çözerseniz konuyu iyice anlamış olursunuz.)
Soru 63:
x2 + y2 + 5x + ky + 4 = 0 çemberinin y eksenine teğet olması için k kaç olmalıdır?
Çözüm:
Çemberin y eksenine teğet olduğu noktada x değeri 0 olacaktır. Denklemde x yerine 0 koyalım;
y2 + ky + 4 = 0 denklemini elde ederiz ki, çember y eksenine teğet olduğu için bu denklemin tek kökü olmalı, yani 
= 0 olmalıdır. a=1, b=k, c=4 olduğuna göre, = b2 – 4ac = 0 k = 
4 bulunur.
Soru 64:
(x-3)2 + (y-4)2 = 9 çemberi ile x2+y2 = k2 çemberinin ayrık olması için k ne olmalıdır?
Çözüm:
Ayrık çemberler, iç içe olmayıp birbirini kesmeyen çemberlerdir.
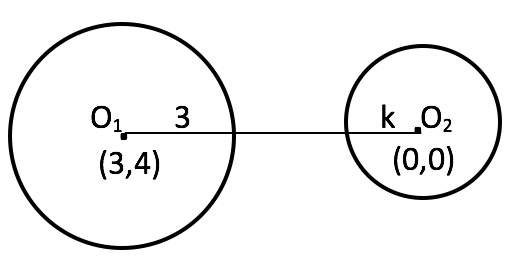
O1O2 > 3 + k olmalıdır. 5 > 3 + k k < 2 olur.
Soru 65:
(2k – 2)x2 + (3k – 4)y2 + 2kx +8y = 0 denklemi bir çember belirttiğine göre çemberin yarıçapı kaç birimdir?
Çözüm:
Çember denkleminde x2 ve y2 nin katsayıları bir olmak zorunda olduğuna göre soruyu çözelim. Önce k’yı bulalım.
2k – 2 = 3k – 4 k = 2
Bulunan bu değeri denklemde yerine koyarsak;
2x2 + 2y2 + 4x +8y = 0 x2 + y2 + 2x +4y = 0
Önceki çözümlere bakarak r’yi siz bulun. (r = 
)