Soru 26:

A(2,3) noktasının B(3,2) noktasına göre simetriği nedir?

Çözüm:

Bu soruyu 2 türlü çözeceğiz. Önce şekli çizelim:

1. Çözüm: A dan B ye absis (2 den 3 e) 1 arttığına göre B den A’ ne de 1 artar, dolayısıyla A’ nün absisi 4 olur. Aynı mantıkla A’ ün ordinatı da 1 olur. A’(4,1)

2. Çözüm: Orta nokta formülü ile;

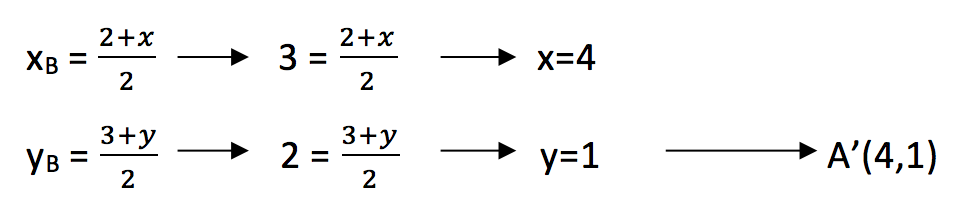
Not: Hangi çözüm kolayınıza gelirse onu kullanın.

---

Soru 27:

A(2,3) noktasının y=x-1 doğrusuna göre simetriğinin koordinatlarını bulun.

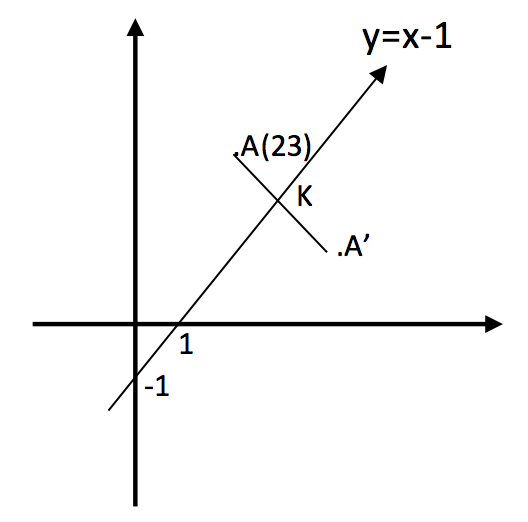
Çözüm:

Bu soruyu 3 adımda çözeceğiz.

1. adım: Önce (2,3) noktasından geçen ve y=x-1 doğrusuna dik olan doğrunun denklemini bulalım: Verilen doğrunun eğimi (x’in katsayısı) 1 olduğuna göre, buna dik olan doğrunun eğimi -1  olduğundan AA’ doğrusunun denklemi;   A(2,3) ve m=-1

y = mx + n        3 = -1.2 + n       n=5       y=-x + 5

2. adım: Ortak çözümle K kesim noktasının koordinatlarını bulalım:

x-1 = -x+5       x=3 ve y=2 olur. K nın koordinatları (3,2)

3. adım: K orta nokta olacağına göre A’ nün koordinatları (4,1) olarak bulunur. İşlemleri siz yapın.

---

Soru 28:

3x-2y+9=0 doğrusunun A(1,2) noktasına göre simetriğinin denklemi nedir?

Çözüm:

Önce 3x-2y+9=0 denklemini  şeklinde yazalım. Bir doğrunun bir noktaya göre simetriği, o doğruya paralel olacağından simetrik doğrunun eğimi de olacaktır. Eğimi bildiğimize göre şimdi yapılacak iş simetrik doğru üzerinde bir noktanın koordinatlarını bulmaktır. Bunun için verilen doğru üzerinde bir nokta alınır ve bu noktanın A(1,2) noktasına göre simetriği alınır. Verilen doğru 3x-2y+9=0 olduğuna göre kolaylık olsun diye (-3,0) noktasını alalım. Bu noktanın A(1,2) noktasına göre simetriği A’(5,4) noktası olur.(Bu değerleri siz de bulun) Eğim ve nokta belli olduğuna göre simetrik doğrunun denklemi:

İsterseniz her 2 tarafı 2 ile çarparak 2y=3x – 7       3x – 2y -7=0 denklemini elde edebilirsiniz.

Not: Sorunun çözümünü daha iyi anlamak için analitik düzlemde doğrunun grafiğini çizin. Simetri noktasını gösterin.

---

Soru 29:

y = 2 doğrusu ile y = x +2 doğrusu arasındaki açı kaç derecedir?

Çözüm:

Şekil çizerseniz çok kısa zamanda çözülecek bir soru olduğunu görürsünüz. Tabii bu arada tan60=olduğunu bileceksiniz.

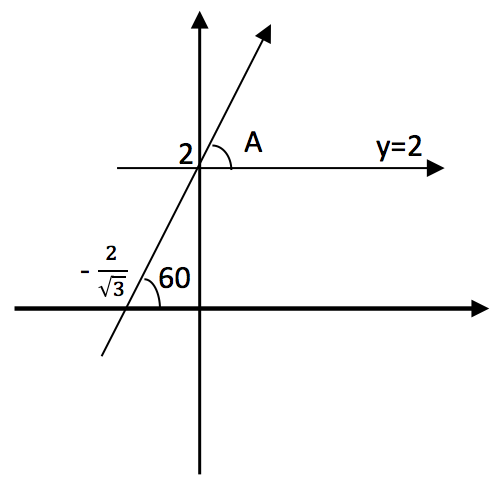
y=x + 2 doğrusunun eğimi olduğundan x ekseni ile yaptığı açı 60⁰ dir. Soruda A açısı sorulmuş.

Doğrunun x ekseni ile yaptığı açı ile A açısı yöndeş olduğuna göre A açısı da 60⁰ dir.

İkinci bir çözüm yolu iki doğru arasındaki açının (α) tanjantını veren formülü kullanmaktır.

tanα =    formülünde m₁=, m₂ = 0 değerlerini yerine koyarsak tanα = olur bu da α = 60⁰ demektir.

 

Not: m₂ nin niye 0 olduğunu anlamayanlara: x eksenine paralel olan doğruların x ekseni ile yaptıkları açı 0⁰ olduğuna göre tan0=0 olacaktır.

(m₁ ve m₂ yer değiştirirse sonuç negatif çıkacaktı. Kesişen 2 doğru arasında biri geniş biri dar 2 açı vardır.)

---

Soru 30:

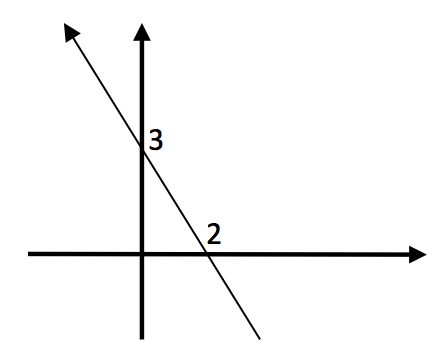F(x) in grafiği yanda verilmiştir. Buna göre f(2x+1) fonksiyonun grafiğini çizin.

 

 

 

 

Çözüm:

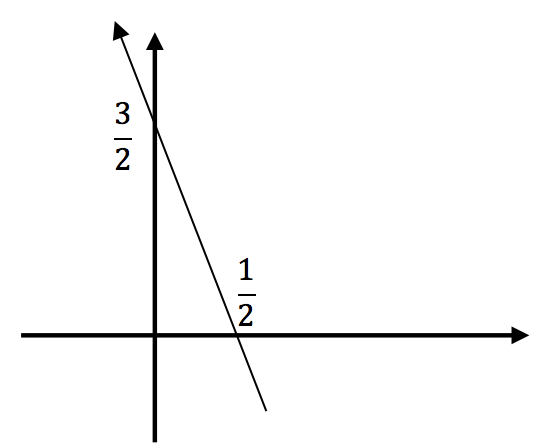
m= –    ve ordinat değeri (n) 3 olduğuna göre doğru denklemi f(x) = y = –x +3 tür. F(2x+1) fonksiyonu ise f(x) fonksiyonunda x yerine 2x+1 konularak elde edilir. F(2x+1) = –(2x+1) + 3 = – 3x + 

(0,) ve (, 0) noktaları bu fonksiyona ait noktalar olduğuna göre grafiği aşağıdaki gibidir.

 

---

< Soru 21 – 25  –  Soru 31 – 35 >

Çözümlü Analitik Geometri Soruları Ana Sayfa