Soru 36:
2x – 3y + 12 = 0 doğrusu ile y = 
x + 2 doğrusuna eşit uzaklıkta olan noktaların geometrik yer denklemi nedir?
Çözüm:
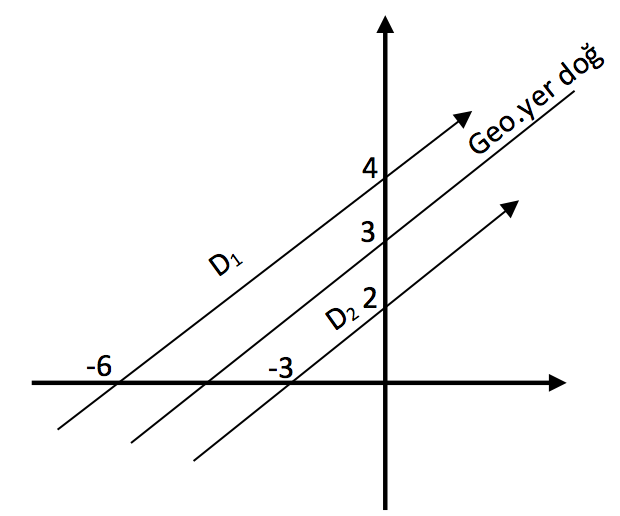
Doğruların grafiklerini çizerek soruyu mantıkla çözelim: Aradığımız geometrik yer doğrusu eğimi olan bir doğru olacaktır. Grafiklere bakarak n değerinin 3 olduğunu görüyoruz. Öyleyse geometrik yer doğrusunun denklemi y =x + 3 olur. Denklemi standart hale getirmek için eşitliğin her 2 tarafını 3 ile çarpalım.
3y=2x+9 
2x-3y +9=0
(Paralel 2 doğruya eşit uzaklıkta olan noktaların geometrik yeri, bu iki doğrunun tam ortasında olan paralel bir doğrudur)
Not: Bu tür soruların da formülü var. Formül severler her soru tipi için ayrı bir formül ezberleyebilirler.
Soru 37:
A(2,4) noktasının y=x doğrusuna göre simetriği B, y=-x doğrusuna göre simetriği C ise BC doğrusunun denklemini bulun.
Çözüm:
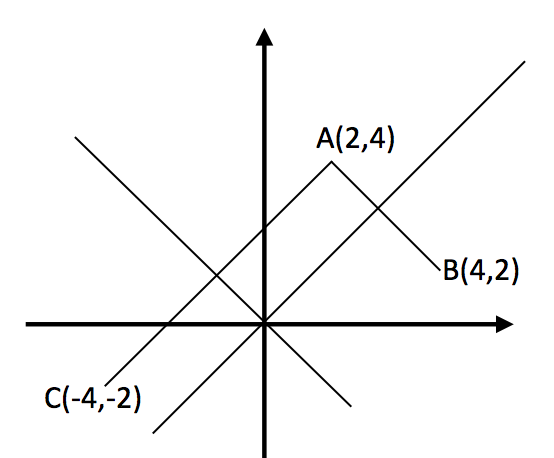
A(a,b) noktasının y=x doğrusuna göre simetriği (b,a) (x ve y yer değiştirdi) y=-x doğrusuna göre simetriği (-b,-a) (x ve y hem yer, hem işaret değiştirdi). Bu kuralları şekil çizerek kendiniz de bulabilirsiniz. Soruya uygun şekil yanda çizilmiştir. Şimdi yapılacak iş BC doğrusunun denklemini bulmaktır. Bunun için mBC’yi bulalım.
bu değeri B’nin koordinatlarıyla beraber y=mx+n denkleminde yerine koyalım;
y=mx+n 2=
.4 +n n=0 olduğuna göre denklem y=x olur.
Soru 38:
Şekildeki ABCD yamuğunun alanı kaçtır?
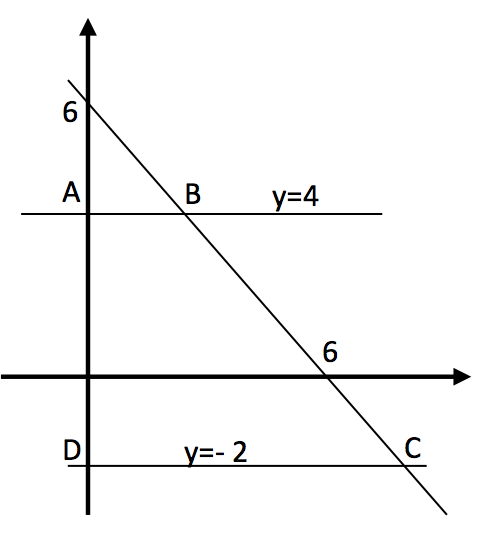
Çözüm:
Önce doğrunun denklemini yazalım;
m=-1 (neden) ve n=6 y=- x + 6
Doğru denkleminde y yerine 4 koyarsak;
4=- x + 6 x=2 buna göre B(2,4) olur.
Doğru denkleminde y yerine -2 koyarsak – 2 = – x + 6 x=8 buna göre de C(8,-2) olur.
Yamuğun alanı= (alt taban+ üst taban).yükseklik
Alt taban: DC= 8, üst taban: AB=2, yükseklik: AD=6
Alan=(8+2).6 =30 olur.
Soru 39:
2x-y-3=0 doğrusu ile 2x-3y+1=0 doğrusu arasındaki açıların tanjantları kaçtır?
Çözüm:
Verilen doğru denklemlerinin eğimlerini bulalım:
2x-y-3=0 y=2x-3 m1=2
2x-3y+1=0 3y=2x+1 y= x+ 
m2= bu değerleri
tanα =
eşitliğinde yerine koyarsak tanα = 
olur. m1 ile m2 yer değiştirirse tanα = – olur. Bunun nedeni kesişen 2 doğru arasında (dik olma durumu hariç) biri dar, biri geniş olmak üzere 2 açı olmasıdır.
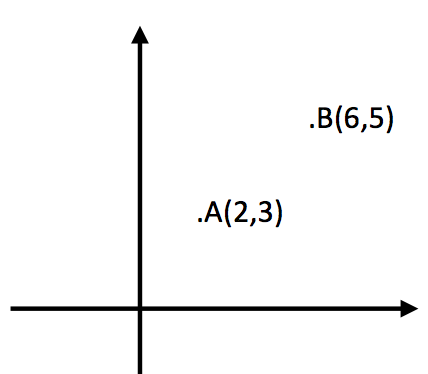
Soru 40:
Yandaki şekilde A ve B noktalarının koordinatları verilmiştir. x ekseni üzerinde öyle bir C noktası bulunuz ki AC+BC toplamı en küçük olsun.
Çözüm:
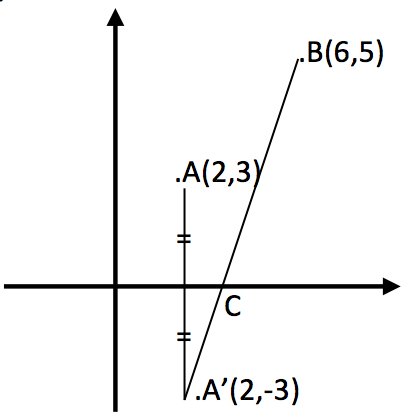
A noktasının x eksenine göre simetriğini alalım; A’(2,-3) olur. A’B doğrusunun x eksenini kestiği nokta aradığımız C noktasıdır. Çünkü 2 nokta arasında en kısa mesafe bu 2 noktayı birleştiren doğru parçasıdır. AC=A’C olduğundan A’C yerine AC yazılabilir. Buna göre de AC+BC toplamı en küçük olur.
Şimdi yapılacak iş A’B doğrusunun denklemini bulmak;
ve B(6,5) noktasını alalım;
y=mx +n 5=2.6+n n=-7 y=2x -7
C noktasında y değeri 0 olacağından x= 
olur. C’nin koordinatları (, 0)
Not: Yukardaki soruyu A’nın değil de B’nin x eksenine göre simetriğini alarak da çözebilirsiniz (Bi zahmet, çözüverin).