Bundan sonraki soruların büyük bir kısmı çemberin analitiği ile ilgili sorular olacaktır. Ders kitaplarında çemberin analitiği ile ilgili birçok formül verilmiştir (formül severlere söyleyecek bir sözümüz yok). Analitik severler ise sadece temel analitik bilgilerle, çemberin analitiği ile ilgili soruların nasıl çözüldüğünü görecekler. Sadece çemberin genel denklemini bileceksiniz ki bu da Pisagor bağıntısından başka bir şey değildir. Merkezin koordinatları (a, b) , çember üzerinde herhangi bir nokta (x, y) olsun. İki nokta arasındaki uzaklık yarıçapı vereceğinden:
Çemberin genel denklemi; (x-a)2 + (y-b)2 = r2 şeklinde olur.
Not: Sitemizdeki sorularda D,E ve F değerlerini çözümlerde kullanmayacağız. Bu harfleri içeren formülleri ezberlemek istemeyenler, çözümlerimizi iyi takip etsinler)
Soru 41:
Denklemi x2 + y2 -4x +2y – 4 = 0 olan çemberin yarıçap uzunluğu nedir?
Çözüm:
D, E ve F kullanmadan soruyu basit eşleştirmelerle çözelim. Çemberin genel denklemini açarak yazalım;
x2 – 2ax + a2 + y2 – 2by + b2 = r2 
x2 + y2 – 2ax -2by +a2 + b2 – r2 = 0
Şimdi de elde ettiğimiz eşitlikle, soruda verilen eşitliği birbirine eşleyelim;
x2 + y2 – 2ax – 2by + a2 + b2 – r2 = x2 + y2 – 4x + 2y – 4
x2 ve y2 nin katsayıları aynı,
-2ax = -4x a=2 ve -2by=+2y b= -1
Yarıçapı bulmak için ise sayı kısımlarını birbirine eşleyelim;
a2 + b2 – r2 = -4 22 + (-1)2 – r2 = -4 r = 3
2.çözüm: x2 + y2 – 4x + 2y – 4 = 0 eşitliğinde;
x2– 4x ‘i elde etmek için, eşitlikte (x-2)2 olmak zorunda
y + 2y ‘ yi elde etmek için de eşitlikte (y+1)2 olmalı,
Bu durumda çember denklemi (x-2)2 + (y+1)2 – 9 = 0 olur. (-9’un nerden geldiğini de siz de bulun)
(x-2)2 + (y+1)2 = 9 r2 = 9 r = 3
Soru 42:
x=-4 ve x = 6 doğrularına teğet olan ve merkezi y-x-3 =0 doğrusu üzerinde olan çemberin denklemi nedir?
Çözüm:
Verilenlere uygun bir şekil çizersek soruyu kolayca çözeriz.
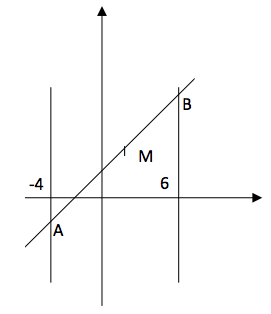
Şekle baktığımızda çemberin çapının 10 olduğunu görüyoruz. Merkezin koordinatlarını bulunca soru çözülmüş olacak. Bunun için A ve B nin koordinatlarını bulmalıyız.
y-x-3=0 denkleminde x yerine -4 koyarsak y=-1 olur. Yani A noktasının koordinatları (-4, -1). Aynı mantıkla B noktasının koordinatları (6, 9) olur. Çemberin merkezi olan M noktası AB doğru parçasının orta noktası (neden?) olacağına göre M’nin koordinatları da (1, 4) olur. Buna göre çember denklemi; (x-1)2 + (y-4)2 = 25
Not: Pratik bir öğrenci A ve B’nin koordinatlarını bulmadan da M’nin koordinatlarını bulabilir. x= -4 ve x= 6 doğrularına eşit uzaklıkta olan doğru x=1 doğrusudur. M noktası x=1 doğrusu üzerinde olacağından M noktasının absisi 1 olur. Bu değer y-x-3=0 denkleminde yerine konursa y=4 bulunur. M(1, 4)
Soru 43:
x2 + y2 – 1 = 0 ve x2 + y2 – 8x + 6y + 21 = 0 çemberleri arasındaki en kısa uzaklık kaç birimdir?
Çözüm:
x2 +y2 – 1 = 0 x2 + y2 = 1 denklemi ile verilen çember merkezil bir çember olup yarıçapı 1 birimdir (merkezi orjinde olan çemberlere, merkezil çember denir).
İkinci denklemi; (x-4)2 + (y+3)2 – 4 = 0 (x-4)2 + (y+3)2 = 4 şeklinde yazabiliriz (bu şekilde yazmakta zorlanıyorsanız 41. sorudaki gibi basit eşleştirmelerle a, b ve r’yi bulabilirsiniz.).
M1(0,0) ve M2(4,-3) olduğuna göre iki çemberin merkezleri arasındaki uzaklık 5 birim (siz de bulun) olur. r1=1 ve r2=2 birim olduğuna göre iki çember arasındaki en kısa mesafe: 5 – (2+1) = 2 birimdir.
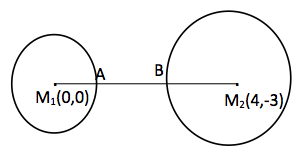
Soruya uygun şekli yukarda görüyorsunuz. İstenen uzaklık AB arasıdır.
Soru 44:
A(0,0), B(8,0) ve C(0,6) noktalarından geçen çemberin denklemi nedir?
Çözüm:
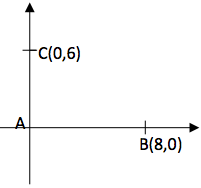
B ile C’yi birleştirdiğimizde elde edilen ABC üçgeni bir dik üçgen olur. A, B ve C noktalarından geçen çemberi çizdiğimizde (siz çizin) BC doğru parçası bu çemberin çapı olur (çünkü bir çemberde çapı gören çevre açı 900 dir.) BC = 10 birim olduğuna göre (neden?) çemberin çapı 10 birim, yarıçapı da 5 birim olur. BC’nin orta noktası da merkez olur. Orta noktanın koordinatları (4,3) olduğundan çemberin denklemi;
(x-4)2 + (y-3)2 = 25
Soru 45:
(x-2)2 + (y-3)2 = 2 çemberine üzerindeki A(3, 2) noktasından çizilen teğetin denklemini bulunuz.
Çözüm:
Bu soru 2 şekilde çözülür. Birinci çözüm yolu temel analitik bilgilerle soruyu çözmektir. Çözelim;
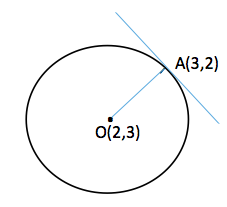Çemberin merkezine O diyelim. O’nun koordinatları O(2,3) olduğuna göre, OA’nın eğimi -1 olacağından (neden?) A noktasındaki teğetim eğimi 1 olur (neden?)
y=mx+n doğru denkleminde değerleri yerine koyarsak; 2=1.3+n eşitliğinden n=-1 olur. Teğet denklemi; y=x-1.
İkinci çözüm yolu türev yardımı ile çözmektir. Temel analitik bilgiler çemberin analitiğinde iş görür, ama elips ve hiperboldeki teğet denklemleri (temel analitik bilgilerle değil) türev yardımıyla kolayca çözülür. Bunun için kapalı fonksiyonun türev kuralını bilmeniz gerekir. Bilmeyenlere kısaca hatırlatalım; Önüne – işareti konmuş bir kesir ifadesinde, x’e göre türev paya, y’ye göre türev de paydaya yazılır. Kapalı fonksiyon türevinde hata yapmaktan korkuyorsanız, önce ifadeyi sıfıra eşitleyecek şekilde düzenleme yapın, x’e göre türev alırken y değerlerini, y’ye göre türev alırken x değerlerini sayı olarak kabul edin.
Örneğin, x2y3 + x2 + y +2016=0 kapalı fonksiyonunun türevi: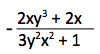 
Sorumuza gelelim; (x-2)2 + (y-3)2 – 2 = 0 ifadesinin x’e göre türevi: 2(x-2).1 ve y’ye göre türevi: 2(y-3).1 olduğundan ifadenin türevi: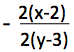 
şeklinde olur, A noktasının koordinatları yerine konursa türev değeri (yani eğim) 1 olur. Birinci çözümdeki gibi devam edilir.