Soru 46:
(x-4)2 + (y+1)2 = 10 çemberine üzerindeki (3,2) noktasından çizilen normal denklemini bulun.
Çözüm:
Bir çemberin normali, verilen noktayı merkeze birleştiren doğrudur. Şekildeki AO doğru parçasının denklemini bulursak, normalin denklemini bulmuş oluruz.
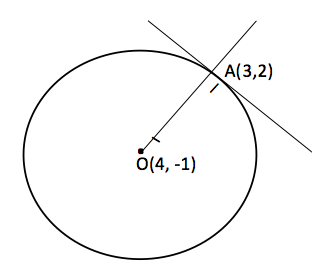
Önce AO’nun eğimini bulalım. 
y= mx+n 
y=-3x+n eşitliğinde A ve O noktalarından herhangi birinin koordinatlarını yerine koyarak n’i bulalım. O(4, -1) olduğuna göre
-1 = -3.4 + n n = 11
Normal denklemi de y = -3x + 11 olur.
Not: Sayısal okuyan öğrencilere; Küresel bir yüzeye gelen ışığın kırıldıktan sonra nasıl bir yol izleyeceğini bulmak için, normali çizmeniz yeterli olacaktır. Normalin ne olduğunu anladığınıza göre, ince kenarlı bir mercekte asal eksene paralel gelen ışığın, neden odaktan geçecek şekilde kırıldığını açıklayınız.
Soru 47:
(x-4)2 + (y-1)2 = 25 çemberinin 8 birim uzunluğundaki kirişlerinin orta noktalarının geometrik yer denklemini bulun.
Çözüm:
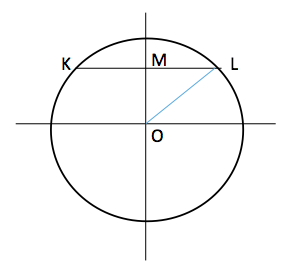
Bu sorunun çözümünde, kirişin orta dikmesi merkezden geçer kuralından faydalanacağız. KL kirişinin orta noktası M olsun. OL=r=5 ve ML=4 olduğu için OM = 3 birim olur. Sonsuz sayıda kirişten, sonsuz sayıda M noktası elde edilir. Bu M noktaları O merkezli, 3 birim yarıçaplı bir çember oluştururlar.
Bu değerlere göre geometrik yer denklemi (x-4)2 + (y+2)2 = 9 olur.
Soru 48:
Bir noktadan eşit uzaklıktaki noktaların geometrik yeri her zaman bir çember midir?
Çözüm:
Noktanın bulunduğu yere göre değerlendirme yapılır. Nokta düzlem üzerinde ve eşit uzaklıktaki noktalar da aynı düzlem üzerinde ise, geometrik yer bir çemberdir.
Uzayda bir noktadan eşit uzaklıktaki noktaların geometrik yeri ise küre yüzeyidir.
Soru 49:
(3m-5)x2 + (m-1)y2 -6x + 2y +3m = 0 ifadesi bir çember belirttiğine göre, çemberin denklemini bulun.
Çözüm:
Bir ifadenin çember belirtmesi için x2 ve y2 nin katsayıları eşit ve 1 olmak zorundadır. 3m-5 = m-1 m=2
m=2 için x2 ve y2 nin katsayıları 1 olduğuna göre, başka bir işleme gerek yok. x2+ y2 -6x + 2y +6 = 0
(x-3)2 + (y+1)2-4 = 0 (-4’ü nereden bulduk?)
Çemberin denklemi; (x-3)2 + (y+1)2 = 4
Uyarı: Bulunan m değeri için x2 ve y2 nin katsayıları 1 olmasaydı, bütün katsayıları m ile bölecektik. (neden?)
Soru 50:
x2 + y2 – 2x + 4y + m denklemi bir nokta belirttiğine göre m kaçtır?
Çözüm: Noktan, yarıçapı sıfır olan çember olarak tanımlanabileceğine göre soruyu çözelim;
Verilen denklemde r = 0 olmalıdır. Eşleştirme metoduyla; a=1, b= -2 bulunur.
a2 + b2 – r2 = m 1 + 4 – 0 = m m = 5 bulunur.
Eşleştirme metodu için 41. soruya bakabilirsiniz.