Soru 51:
x2 + y2 = 2 çemberi ile y = mx + 2 doğrusu birbirine teğet ise m’ nin değeri kaçtır?
Çözüm:
Bu tür sorular 2. derece denklemlerden bildiğiniz 
kavramıyla kolayca çözülür. x2 + y2 =2 denkleminde y yerine (mx +2) yazarak ortak çözüm yapalım.
x2 + (mx + 2)2 = 2 
x2 +m2x2 +4mx +4 – 2 = 0
(m2 + 1 )x2 +4mx +2 = 0 Bu denklemde a=m2+1, b=4m ve c=2 olduğuna göre;
Doğru çembere teğet olduğundan ortak çözümün 1 tane kökü olması gerekir ki bunun için = 0 olmalıdır. = b2 – 4ac eşitliğinden,
16m2 – 4.(m2 + 1).2 = 0 m = 
1 olur.
Soru 52:
x2 + y2 – 4x -2ky + 3k – 9 = 0 çemberi orjinden geçtiğine göre, yarıçap uzunluğu kaçtır?
Çözüm:
Oldukça kolay bir soru. Çember orjinden geçtiğine göre, orjinin koordinatları (0,0) denklemi sağlar. x ve y gördüğümüz yere 0 yazarsak k=3 bulunur. Buna göre çemberin denklemi;
x2 + y2 – 4x – 6y = 0 olur. Yarıçap uzunluğu da 
olur.
(Önceki çözümlere bakarak soruyu siz çözün.)
Soru 53:
y = mx + 2 doğrusunun x2 + y2 = 2 çemberi üzerinde bir kiriş ayırması için m ne olmalıdır?
Çözüm:
Bir doğrunun bir çember üzerinde kiriş ayırması demek; doğrunun çemberi 2 noktada kesmesi demektir. Bu durumda yapılması gereken, ortak çözümde >0 olacak şekilde işlem yapmaktır.
Ortak çözüm için çember denkleminde y yerine mx+2 koyalım.
x2 + (mx+2)2 = 2 x2 + m2x2 + 4mx + 2 = 0
(m2+1)x2 + 4mx + 2 = 0 eşitliğinde: a=m2+1, b=4m, c=2 olduğuna göre
= b2 – 4ac = 16m2 – 4.(m2+1).2 =8m2– 8 dir. >0 olacak şekilde işaret tablosunu yapalım;
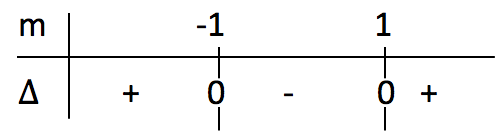
İşaret tablosuna göre m<-1 ve m>1 olmalıdır. (m=-1 ve m=1 için doğru çembere teğet olur, neden?)
Soru 54:
x2+ y2 – 6x = 0 çemberinin üzerindeki A(2, 2
) noktasından geçen çapın öteki uç noktası B’nin koordinatları nedir?
Çözüm:
Çemberin merkezinin koordinatlarını bulursak soru çözülmüş olur. Eşleştirme yöntemine göre a=3 ve b=0 olur. Veya yukardaki eşitliği (x – 3)2 + (y – 0)2 = 0 şeklinde yazarak da merkezin koordinatlarını bulabiliriz. Merkez AB’nin orta noktası olacağına göre;
= 3 xB = 4 ve aynı mantıkla yB = -2 bulunur. Yani aranılan nokta; B(4, -2) dir.
Soru 55:
x2 + y2 – 4y + m = 0 çemberinin x = 3 doğrusuna teğet olması için m kaç olmalıdır?
Çözüm:
Eşleştirme yöntemine göre; a=0 ve b=2 dir. Merkezin koordinatları (0, 2) ve yarıçap 3 olduğuna göre çemberin denklemini yazarsak; x2 + (y-2)2 = 9 x2 + y2 – 4y + 4 – 9 = 0 m = -5 (yarıçapın niye 3 olduğunu anlamayanlara; (0, 2) noktasının x = 3 doğrusuna uzaklığının 3 olduğunu belirtelim.)
Çözümü bir de yardımıyla yapalım. Çember x = 3 doğrusuna teğet olduğuna göre çember denklemi ile doğru denkleminin ortak çözümünde = 0 olmalıdır. Buna göre çember denkleminde x yerine 3 koyalım.
32 + y2– 4y + m = 0 y2 – 4y + m + 9= 0 bu ikinci derece denklemde; a = 1, b = -4 ve c = m + 9 olduğuna göre = 0 m = -5 (İşlemi siz tamamlayın)