Soru 56:
M(2, -1) merkezli ve yarıçapı 2![]() olan çemberin y ekseni üzerinde ayırdığı kiriş kaç birimdir?
olan çemberin y ekseni üzerinde ayırdığı kiriş kaç birimdir?
Çözüm:
Çemberin denklemi; (x – 2)2 + (y + 1 )2 = 20 olduğuna göre x yerine 0 koyalım (neden?).
4 + (y + 1)2 = 20 ![]() (y + 1)2 = 16
(y + 1)2 = 16 ![]() |y+1| = 4 eşitliğinden y1=3 ve y2 = -5 bulunur.
|y+1| = 4 eşitliğinden y1=3 ve y2 = -5 bulunur.
(0, 3) ve (0, -5) noktaları arasındaki uzaklık 8 birim olacağından kirişin uzunluğu 8 birimdir.
Soru 57:
(x-m)2 + y2 = 1 çemberi ile x2 + (y-3)2 = m2 çemberi birbirine dıştan teğet ise m kaçtır?
Çözüm:
Çemberler dıştan teğet ise merkezler arası uzaklık yarıçapları toplamına eşit olur.
Birinci çemberin merkezi M1(m, 0), yarıçapı r1 = 1
İkinci çemberin merkezi M2(0, 3), yarıçapı r2 = m
Merkezler arası uzaklık (yani 2 nokta arasındaki uzaklık)
![]() = m + 1
= m + 1 ![]() her 2 tarafın karesini alalım;
her 2 tarafın karesini alalım;
m2 + 9 = m2 + 2m +1 ![]() m = 4 olur.
m = 4 olur.
Not: Çemberler içten teğet olursa merkezler arası uzaklık d=|r1-r2| olur.
Soru 58:
(x-1)2 + (y+2)2 = 22 çemberine K(-6, 1) noktasından çizilen teğetin uzunluğu kaç birimdir?
Çözüm:
Çemberin analitiği ile harmanlanmış kolay bir pisagor bağıntısı sorusu. Verilenlere göre şekil çizelim:
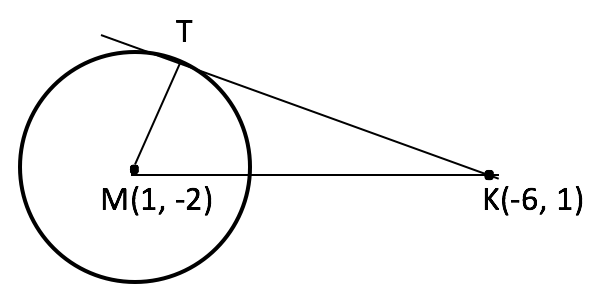
KTM bir dik üçgen olacağına göre (neden) kenar uzunluklarından faydalanarak KT uzunluğunu bulacağız. KM = ![]() (işlemi siz yapın) ve MT =
(işlemi siz yapın) ve MT = ![]() olduğuna göre pisagor bağıntısından KT = 6 bulunur.
olduğuna göre pisagor bağıntısından KT = 6 bulunur.
( K noktasından çembere uzunlukları eşit olan 2 teğet çizilir.)
Soru 59:
A(3, 4) noktasının y = mx + 2 doğrularına göre simetriklerinin geometrik yer denklemi nedir?
Çözüm:
m kaç olursa olsun, doğruların hepsi (0, 2) noktasından geçer.
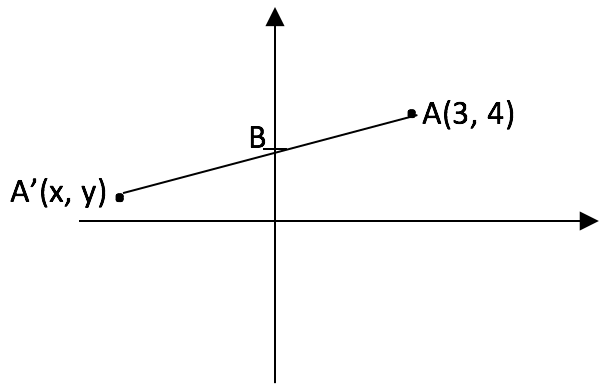
Bu durumda A noktasının B noktasına göre simetriği A’(x, y) olsun. B noktasının koordinatları (0, 2) olduğuna göre A’B2 = BA2 eşitliğini yazalım.
A’B2 = (x-0)2 + (y-2)2 ve BA2 = (3-0)2 + (4-2)2 ![]() x2 + (y-2)2 = 13
x2 + (y-2)2 = 13
Demek ki geometrik yer bir çembermiş.
(Bazı öğrenciler geometrik yer sorularını sevmezler. Halbuki geometrik yer soruları oldukça kolay olup, bütün mesele x ve y arasında bir ilişki kurabilmektir. Sınavlarda geometrik yer sorularını kaçırmayın.)
Soru 60:
Merkezi 2y – x – 4 = 0 doğrusu üzerinde olan, orjin ve A(4, 0) noktalarından geçen çemberin denklemi nedir?
Çözüm:
Soruya uygun şekli incelerseniz, OA nın kiriş olduğunu görürsünüz. Çember sorularında çok kullanılan bir özellik olan, kirişin orta dikmesi merkezden geçer özelliği ile soruyu kolayca çözebiliriz.
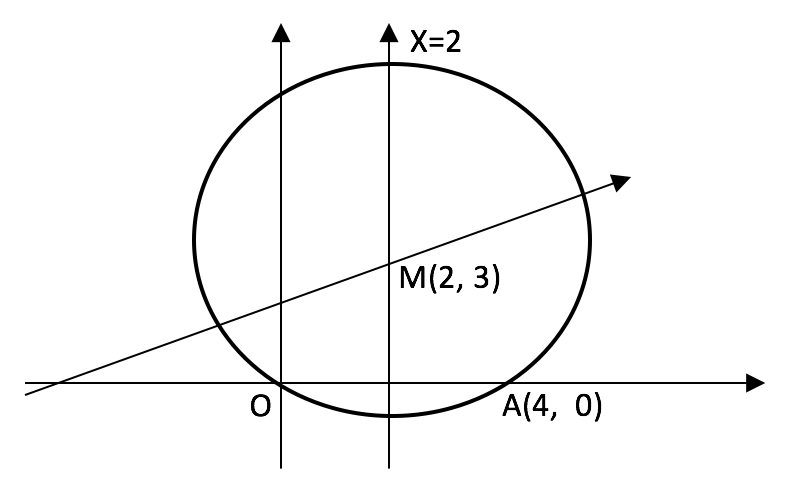
Kirişin orta dikmesi x=2 doğrusu olup merkezin absisi 2 dir. Bu değeri doğru denkleminde yerine koyarsak, y=3 olur. Yani merkezin koordinatları (2, 3) olup yarıçap ![]() tür. (neden?)
tür. (neden?)
Çemberin denklemi de (x-2)2 + (y-3)2 = 13 olur.