Soru 11:
A(1,3) noktasını orjine birleştiren doğrunun denklemi nedir?
Çözüm:
Orjinin koordinatları (0,0) olduğuna göre doğrunun eğimi;
m= 
= 3 olur. Orjinden geçen doğrunun ordinat değeri n=0 olacağından doğru denklemi y = 3x olur.
Not: Analitik düzlemde A noktasını işaretleyerek eğimi tanjant değeri olarak da bulabilirsiniz.
Soru 12:
kx + 2k -2x +y – 1 = 0 doğrularının geçtiği sabit noktanın koordinatları nedir?
Çözüm:
Bu tür sorularda k’ya 2 ayrı uygun değer verilerek 2 denklem elde edilir. Ortak çözümle sonuca gidilir. Uygun değerden maksat çözümü kolaylaştıracak değerlerdir. Bu soruda k’ya verilecek ilk uygun değer 2 dir. Çünkü k’ya 2 değeri vererek x’leri yok ederiz.
2x + 2.2 – 2x +y -1 =0 eşitliğinden y= -3 bulunur. Şimdi de k’ya 0 vererek x değerini bulalım:
0.x + 2.0 -2x + y -1 = 0 
y= -3 için x = -2 bulunur. İstenilen noktanın koordinatları (-2,-3) olur.
Soru 13:
3x-4y=6 doğrusuna paralel olan ve A(4,-1) noktasından geçen doğrunun denklemi nedir?
Çözüm:
A(4,-1) noktasından geçen doğru, 3x-4y=6 doğrusuna paralelse eğimleri birbirine eşittir.
3x-4y=6 doğrusunun eğimini bulalım;
3x-4y=6 4y=3x+6 y= 
x + 
m =
Şimdi de noktası ve eğimi verilen doğru denklemini bulalım:
y=mx+n y=x + n -1 =.4 + n n= -4
Doğru denklemi y =x – 4 şeklinde olur.
Soru 14:
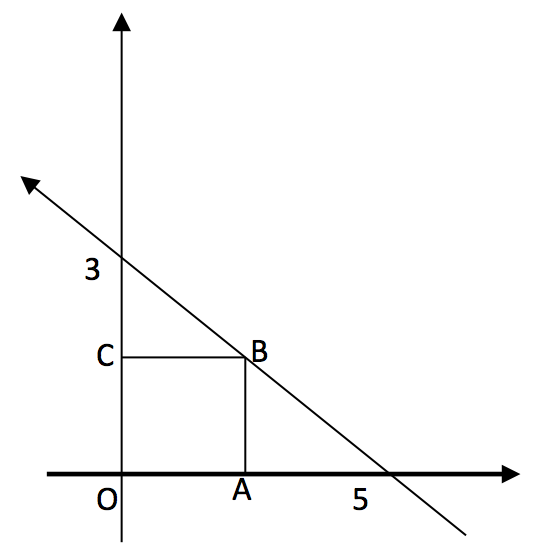Yandaki şekilde OABC bir kare olduğuna göre alanını bulun.
Çözüm:
OABC bir kare ise B noktasında absis ve ordinat birbirine eşittir.
Doğrunun denklemi y= – 
x + 3 olduğuna göre (siz de bulun) B noktasında x=y olduğundan bu eşitliği denklemde yerine koyalım.
x = –x + 3 x = 
Karenin alanı = 
Soru 15:
2kx + 2x + ky +2y + k – 1 = 0 doğrularının geçtiği sabit noktanın koordinatları nedir?
Çözüm:
Biliyorsunuz, bu tür sorularda k’ya 2 ayrı uygun değer vererek ortak çözümle sonuca gidiliyordu. Uygun değerleri saptamadan önce eşitlikte düzenlemeler yaparsanız soruyu daha kısa bir zamanda çözersiniz.
Yukardaki eşitliği x(2k+2) + y(k+2) +k -1 = 0 şeklinde yazarsak k’ya verilecek uygun değerler kendiliğinden ortaya çıkar.
k=-1 için x ler yok olur. y-2=0 y=2
k= -2 için y’ler yok olur. -2x – 3 = 0 x= –
Sabit nokta (- , 2)